How Many Different Hands Are there in Cribbage?

There are 12,994,800 unique hands in cribbage. How do we arrive at that number? The combinatorics calculation to find all the possible 5-card combinations is “52 choose 5,” or this:

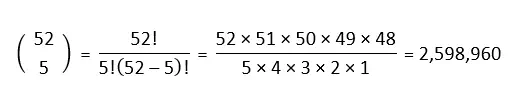
( 52 ¦5 ) = 52! /5! (52 – 5 )! = 52 × 51 × 50 × 49 × 48 /5 × 4 × 3 × 2 × 1 = 2,598,960

However, one card is the cut, which means that for all 2,598,960 possible 5-card combinations, there are 5 unique cribbage hands. Accounting for cuts, there are 2,598,960 × 5 = 12,994,800 unique hands.

What Are the Most Common and Least Common Hand Scores?

The least common score is the legendary 29, made up of 555J in the hand and a 5 cut whose suit matches the J. In all, there are 4 possibilities, 1 for each suit of the 5 cut, for a probability of ~0.00003%, or odds of 3,248,700 : 1 against (i.e., 3,248,700 other hands for every 29-point hand).

The most common score is 4 points, with 2,855,676 possibilities, a probability of ~21.98%, or odds of ~4.55 : 1 against. In a close second for most common score is 2 points, which has 2,813,796 possibilities. Probability for 2 points is ~21.65%, or ~4.62 : 1 against.

These figures are based on the naked theoretical probabilities for 4 cards and 1 cut. In reality, the probability of each score is dependent on the player’s choice of discards. For a rational player, assume that the true probability of ending up with high-scoring hands is greater in real life than these figures suggest. For this reason

How Can I Figure Out My Odds of Improving?

Figuring out your odds of improving your hand with the cut is quite simple, and there’s even a shorthand you can use. After you’ve seen 6 cards (and discarded 2), there are 46 cards left in the deck. Each card represents about 2.17% of the remaining deck, which is more specific than you need to estimate at the table. Let’s round it to a nice, clean 2%.

What this means is that you can quickly ballpark your chances of improving just by counting the cards that improve your hand. When you’re done counting, double that number. This is the approximate percent of the time your hand will improve. The true percent will always be a little higher, since we’ve rounded down by 0.17%.

For example, say you’re dealt A♥3♠4♣9♥T♣K♦. You discard 3♠9♥, leaving you with A♥4♣T♣K♦. How many cuts improve this hand? Any A (3), 4 (3), 5 (4), T (3), J (4), Q (4), or K (3) will improve this hand, for 24 outs in all. Using the shorthand method, that’s about a 48% chance to improve. (The long way, it’s ~52.17%.) This method’s biggest potential inaccuracy is 8 percentage points, in a case like A234, regardless of suits. This hand is worth 4 points on its face, but in reality it’s worth a minimum of 6 points after the cut because all the remaining cards improve it in some way:

Any A, 2, 3 or 4 improves the hand to 10 points.
Any 5 improves it to 7 points.
Any 6 or 7 improves it to 6 points.
Any card 8 or higher improves it to 8 points.

All remaining 46 cards improve the hand, which gives us 92%, whereas the real probability is 100%.

Is There An Easy Way to Find My Expected Score?

Unfortunately, there’s no truly easy way. Knowing your winning chances isn’t the same as knowing how many points you’re likely to get, and figuring that out is substantially more difficult than doubling your number of outs to get that ballpark percent.

To find that, you’d multiply the probability of receiving a particular card—in decimal or fraction form, not percent form—by the number of points you’d get for that card. When you’ve done this for all your potential outs, add up the results. That’s your average improvement from the cut, and it’s how cribbage software figures out which discards are best.

Since we’ve mostly broken it down for A234 already, let’s work it out for that hand, assuming you’ve discarded an 8 and a T.

Any A, 2, 3 or 4 improves the hand to 10 points: (12/46) × 10 ≈ 2.6
Any 5 improves it to 7 points: (4/46) " × 7 ≈ 0.6
Any 6 or 7 improves it to 6 points: (8/46) × 7 ≈ 1.2
Any card 8 or higher improves it to 8 points: (22/46) × 7 ≈ 3.8

In all, the hand is worth an average of about 2.6 + 0.6 + 1.2 + 3.8 = 8.2 points after the cut—not bad considering it only counts up to 4 points before the cut.

Can you think of another hand that always improves with the cut? How much is it worth on average?

Author - Jim Donahue