How Do You Count So Fast in Cribbage?

One of the first things I nailed down as a young cribbage enthusiast was counting hands. Something about it appealed strongly to the pattern-seeker in me. I went to bed many nights dreaming of cribbage hands and how to count them, until I had accounted for all the possible scores and developed shortcuts for the common ones. This somehow helped me sleep.

Counting quickly is good for more than just speeding up the game or helping you sleep. It enables you to make better on-the-fly decisions, which is especially important in a timed format, like online. In a live setting, it also makes you a lot better at spotting an opponent’s miscounted hand.

There’s one basic skill that you’ll use a lot more than others, so let’s start there.

How Many Ways Can You Make 15?

There are six ways you can make 15 with two cards: 5T, 5J, 5Q, 5K, 69, and 78. These are only three unique combos for the purpose of counting; all but two of them are just a 5 and a 10-value card.

The two-card 15s are novice cribbage knowledge. What will get your counting to the next level is internalizing all the three-card combos.

It can help to think of the three-card 15s as subsets of the two-card 15s. It’s a pretty straightforward application of the associative property from grade school (the one that lets you group and ungroup numbers), and it gets simpler once you think of it that way.

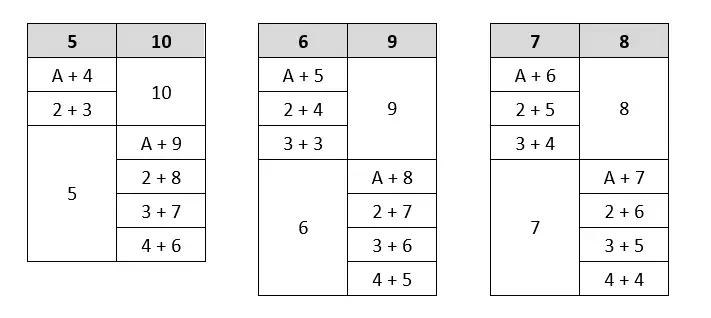
All of the possible three-card 15s are laid out in the table, shown as subsets of the two-card 15s. The number 10 stands for any 10-value card.

5	10
A + 4	10
2 + 3
5	A + 9
	2 + 8
	3 + 7
	4 + 6

6	9
A + 5	9
2 + 4
3 + 3
6	A + 8
	2 + 7
	3 + 6
	4 + 5

7	8
A + 6	8
2 + 5
3 + 4
7	A + 7
	2 + 6
	3 + 5
	4 + 4

The reason I’ve laid it out like this is pertinent: every value within a column is always equal to the number above it. All I’ve done in each case is freeze one number and decompose the other into the handful of pairings that add up to it. And that’s the way I recommend thinking about three-card 15s.

If you have a 5 in your hand, think: what are all the ways I can make 10? Do I have any?

If you have a 6 in your hand, think: what are all the ways I can make 9? Do I have any?

And so on. It’s not the easiest thing at first, but if you add this to your repertoire, it should gradually become automatic when you see these groupings of cards.

The reason this is a foundational skill is because (a) you have to count 15s all the time in this game, and (b) you have to count 15s separately to use a lot of the shortcuts.

It’s true that you can also make 15 with combinations of four cards. Once you’ve internalized the logic of the three-card 15s, the four-card 15s should become that much easier. If you can quickly recognize that A + 2 + 3 = 3 + 3 = 6, it’s clear why A239 makes a 15.

Fortunately, four-card 15s are significantly rarer than three-card 15s, and five-card 15s are rarer still. When you have them, it’ll slow you down, and there’s no real shortcut for that. However, if you apply the same grouping logic as you do for three-card 15s, it will help speed you along.

What Shortcuts Can I Use to Count Complex Runs?

Counting hands that contain a complex run—i.e., a run with a pair or more in it—can be time-consuming. If this eats up your cribbage-playing time, I’ll try to fix that for you today.

There are only four unique complex run counts in the whole game. Once you’ve learned to identify them, you’ll never have to manually count them again.

These shortcuts work regardless of the values of the cards, but they only count the runs and the pairs. You’ll have to count 15s, flushes, and nobs independently.

8-Point Runs: AABC, ABBC, ABCC

Any three-card run that contains a pair is always worth 8 points
Example: 6♠6♥7♠8♥, cut K♥ (AABC structure)
6♠7♠8♥ is a run for 3 points.
6♥7♠8♥ is a run for 3 points.
6♠6♥ is a pair for 2 points.
7♠8♥ is 15 for 2 points.
Runs and pairs total 3 + 3 + 2 = 8. The 15 is worth 2 more. Total is 8 + 2 = 10.

10-Point Runs: AABCD, ABBCD, ABCCD, ABCDD

Any four-card run that contains a pair is always worth 10 points.
Example: T♣J♣Q♠K♦, cut Q♣ (ABCCD structure)
T♣J♣Q♠K♦ is a run for 4 points.
T♣J♣Q♣K♦ is a run for 4 points.
Q♠Q♣ is a pair for 2 points.
J♣ is nobs for 1 point.
Runs and pairs total 4 + 4 + 2 = 10. Nobs is worth 1 more. Total is 10 + 1 = 11.

15-Point Runs: AAABC, ABBBC, ABCCC

Any run that contains trips is always worth 15 points.
Example: A♣2♦2♥3♥, cut 2♠ (ABBBC structure)
A♣2♦3♥ is a run for 3 points.
A♣2♥3♥ is a run for 3 points.
A♣2♠3♥ is a run for 3 points.
2♦2♥2♠ is trips for 6 points.
Runs and pairs total 3 + 3 + 3 + 6 = 15. There is nothing else to score.

16-Point Runs: AABBC, AABCC, ABBCC

Any run that contains two pair is always worth 16 points.
Example: 9♠9♥T♥J♠, cut J♣ (AABCC structure)
9♠T♥J♠ is a run for 3 points.
9♠T♥J♣ is a run for 3 points.
9♥T♥J♠ is a run for 3 points.
9♥T♥J♣ is a run for 3 points.
9♠9♥ is a pair for 2 points.
J♠J♣ is a pair for 2 points.
Runs and pairs total 3 + 3 + 3 + 3 + 2 + 2 = 16. There is nothing else to score.

Not only will remembering these patterns speed up your scoring, but you can use them to estimate your potential gain if you hold part of the pattern. For example, 99TT gives you 8 outs to a 16-point run.

Can you think of other ways to use these shortcuts?

Author - Jim Donahue

Continue Reading...

Quick Counting in Cribbage - Part 1 (this)

Quick Counting in Cribbage - Part 2

Quick Counting in Cribbage - Part 3

Play Cribbage JD Online

More games

JD Software LLC